QUESTION: 

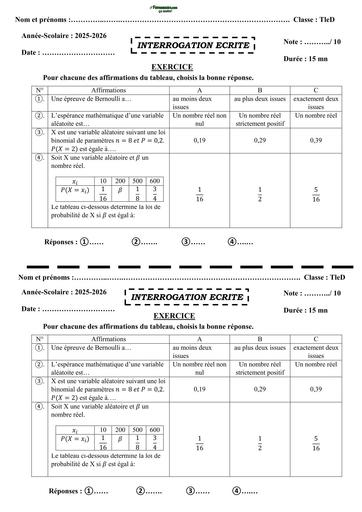
Deux capitaux dont la somme est égal à 50000f , le premier est placé à T% et le second ( T-1)% , l'intérêt annuel produit par le premier est égal à 1500f et le second à 1800f .

1) exprimer les deux capitaux en fonction de T 

2) calculer les deux capitaux puis les deux taux

REPONSE

La première partie

La compréhension de l'exercice

1) Exprimer les deux capitaux en fonction de T :
Soit C1 le premier capital placé à T% et C2 le second capital placé à (T-1)%. Vous avez la somme totale des capitaux, qui est de 50000f. Donc, vous pouvez écrire l'équation suivante :

C1 + C2 = 50000

Maintenant, vous avez également les intérêts annuels produits par chaque capital. L'intérêt annuel pour le premier capital est de 1500f, et pour le second capital, c'est 1800f. Les intérêts se calculent en utilisant la formule : Intérêt = (Capital * Taux d'intérêt) / 100.

Pour le premier capital (C1), vous avez : 1500 = (C1 * T) / 100
Pour le second capital (C2), vous avez : 1800 = (C2 * (T-1)) / 100

Maintenant, vous avez deux équations avec les deux inconnues C1 et C2 en fonction de T. Vous pouvez les résoudre pour exprimer C1 et C2 en fonction de T.

2) Calculer les deux capitaux puis les deux taux :
Vous avez maintenant un système de deux équations à deux inconnues. Vous pouvez utiliser ces équations pour résoudre les valeurs de C1 et C2 en fonction de T. Une fois que vous avez trouvé les valeurs de C1 et C2, vous pouvez également calculer les taux d'intérêt correspondants (T% et (T-1)%).

En résumé, la première étape consiste à exprimer les capitaux en fonction de T en utilisant les informations sur les intérêts annuels. Ensuite, vous résolvez le système d'équations pour trouver les valeurs de C1 et C2. Enfin, vous pouvez calculer les taux d'intérêt correspondants en utilisant les valeurs trouvées.

Deuxième partie

La résolution de l'exercice en question

Pour résoudre ce problème, nous pouvons utiliser les informations données pour établir deux équations et résoudre ensuite pour les deux capitaux et les deux taux.

1) Exprimons d'abord les deux capitaux en fonction de T :

Soit C1 le premier capital en francs et C2 le second capital en francs.

Nous avons les informations suivantes :

- La somme des deux capitaux est égale à 50000f : C1 + C2 = 50000.

- Le premier capital est placé à T% d'intérêt annuel, ce qui signifie que l'intérêt annuel produit par le premier capital est égal à 1500f. Nous pouvons utiliser la formule de l'intérêt simple : Intérêt = (Capital × Taux d'intérêt) / 100. Donc, pour le premier capital : 1500 = (C1 × T) / 100.

- Le second capital est placé à (T-1)% d'intérêt annuel, ce qui signifie que l'intérêt annuel produit par le second capital est égal à 1800f. De même, pour le second capital : 1800 = (C2 × (T-1)) / 100.

Maintenant, nous avons un système de deux équations à deux inconnues :

Équation 1 : C1 + C2 = 50000
Équation 2 : (C1 × T) / 100 = 1500
Équation 3 : (C2 × (T-1)) / 100 = 1800

2) Pour résoudre le système, nous pouvons d'abord utiliser l'équation 2 pour exprimer C1 en fonction de T :

(C1 × T) / 100 = 1500
C1 × T = 1500 × 100
C1 = 150000 / T

Ensuite, utilisons l'équation 3 pour exprimer C2 en fonction de T :

(C2 × (T-1)) / 100 = 1800
C2 × (T-1) = 1800 × 100
C2 × (T-1) = 180000

Maintenant, nous pouvons substituer l'expression de C1 dans l'équation 1 :

(150000 / T) + C2 = 50000

Maintenant, nous pouvons résoudre pour C2 :

C2 = 50000 - (150000 / T)

Maintenant, nous avons les expressions pour les deux capitaux en fonction de T :

C1 = 150000 / T
C2 = 50000 - (150000 / T)

Pour calculer les deux capitaux, nous pouvons choisir une valeur de T, puis utiliser ces expressions pour trouver C1 et C2. Une fois que nous avons les capitaux, nous pouvons calculer les deux taux en utilisant les équations données dans les informations initiales.